Introduction to ensemble data assimilation
Data assimilation is a powerful and widely used computational technique that has many application areas throughout mathematics and science. At a very high level, data assimilation refers to the process of merging prior forecasts with new observations, creating a new analysis that is an “optimal” blending of the two by taking into account their relative uncertainties.
The following animated graphic describes the data assimilation process at a high level:
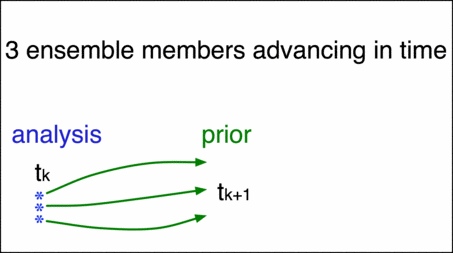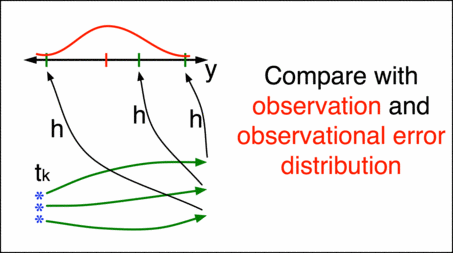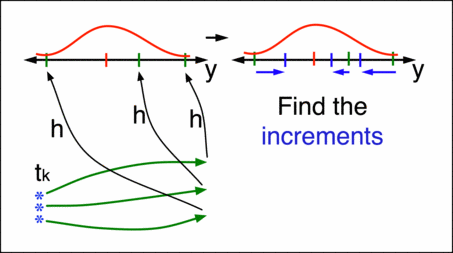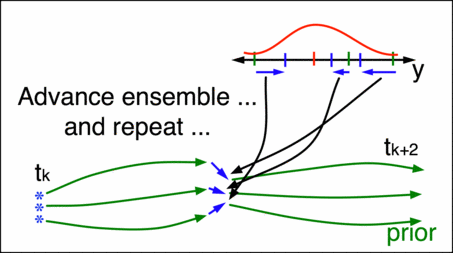
Shown here are three ensemble members, each of which gives a different initial prediction at the time \(t_k\). Moving these predictions forward in time to \(t_{k+1}\) will give a new forecast distribution called a prior.
Suppose at this time there is also an observation, which will have some uncertainty due to instrument noise, etc. Mapping each of the ensemble members to the observations with a function \(h\) and applying Bayes’ theorem will generate an update to the prior distribution, called here the state increment. Adding the state increment to the ensemble members will give the new analysis (also known as the posterior) at time \(t_{k+1}\). This process can then be repeated for each set of observations as many times as necessary. For an introduction to Bayes’ theorem, see Conditional probability and Bayes’ theorem in the Theory section.
Expanding on this somewhat, the \(ith\) ensemble member is denoted \(x_i\) at the present time step. In the above graphic, there were three ensemble members, but in general there are usually many more, typically in the range of 20-1000 depending on the application. Each member \(x_i\) can have \(n\) components which together make up the model state. Each member contains all the variables you want to find the best fit for at a particular time. These variables are usually physically meaningful quantities; for example, this might include the 3D values of water vapor, temperature, wind speed, etc. for an atmospheric model. These values are expected to be advanced forward in time by a model, which is why they are called the “model state.”
Note
In data assimilation, the “model state” is the minimum amount of information necessary to restart the model for a new forecast.
At any particular time step there may be \(m\) observations available. These observations are assumed to relate to the model state and provide “real world” checks against the model forecast. A “forward operator”, represented in the above diagram by \(h\), is a relationship that computes what an observation is most likely to be given a model state. In other words, \(h\) maps between \(x_i\) and \(y_j\), giving the “expected observation” of the \(jth\) observation given the \(ith\) ensemble member. An observation may be of the same quantity as one found in the model state at a particular location, in which case the \(h\) function mapping them is trivial and the comparison is simple. The vector \(y\) may also contain more complex derived functions of the state \(x\) (for example, radar observations of precipitation), in which case the \(h\) function that models this mapping between \(x\) (in this example precipitation) and \(y\) (in this example radar returns) may be an algorithm that is quite complicated.
In practice, observations are never 100% reliable. The observations themselves will have some uncertainty for example arising from instrument noise. The instrument noise error variances are typically published by the instrument manufacturer, and these observation errors are usually assumed to be independent as true instrument “noise” should not be correlated in time or space. Furthermore, since models have a finite resolution (i.e. they are “fuzzy”), there is almost always an error that arises when comparing the model to the observations. This is called the representativeness error. Put together, the potential “likelihood” of the possible values of the observation forms the observational error distribution in the above graphic.
Finally, note that in real-world applications there are typically many fewer observations than state variables, i.e. \(m\) is typically much much less than \(n\). In practice this means that the observations alone cannot be relied upon to predict the model state; the ensemble approach with Bayes’ theorem is necessary.
DART makes it easy to find the optimal solution to the above problem using an ensemble filter algorithm (the most typically used algorithm is the Ensemble Adjustment Kalman Filter; see Important capabilities of DART for more information). The user specifies which state variables make up the \(x\) ensemble vectors, which observations make up the \(y\) vector, and the observation error variances. The ensemble of model states is assumed to be representative of the uncertainty or spread in the model state. Finally, the user tells DART how to advance the model from one forecast to the next. Once DART has this information, it can proceed with optimally blending the observations and model forecasts — in other words, performing data assimilation.
The spread of the ensemble informs DART of the uncertainty in the model state. This allows for as rich, complex, and meaningful relationships as the data contained within the ensemble itself. By default, no implicit assumptions about the relative uncertainties are required, as the data can speak for itself. Areas of large uncertainty will naturally have large spread, as the ensemble members will contain very different values at those locations, while areas of low uncertainty will naturally have low spread due to the ensemble having relatively similar values at those locations. Furthermore, relationships in space and between variables can also be meaningfully derived. Of course this means that the quality of the ensemble is crucial to the success of the DA process, as uncertainty can only be accurately quantified if the ensemble is representative of the “true” uncertainty inherent in the system. Due to the fact that a relatively small number of ensemble members are typically used, estimated correlations between two distant locations may become unreliable due to sampling error. Thus, various techniques such as covariance localization may be employed to improve the quality of estimated relationships and increase skill in prediction. Furthermore, the ensemble spread may sometimes be deemed “too small” or “too large” by various criteria, in which case a multiplicative or additive inflation or deflation, respectively, may be applied. In practice the ensemble method is usually far more accurate and less error-prone than the main alternative of manually specifying uncertainty by some manually-designed algorithm, and it is certainly less labor-intensive to develop.
This was a brief introduction to the important concepts of DA. For more information, see the DART Tutorial and the DART_LAB Tutorial.