Important capabilities of DART

In this section we discuss the capabilities of DART that may be of interest to the user. This is a partial list of all of the functionality that is available in DART, and additional capabilities and improvements are continually being added.

As mentioned above, DART allows for both OSSE and OSE systems of models large and small. This allows users to test both theoretical limits of DA, models, and observations with idealized experiments as well as to improve actual real-world forecasts of chaotic systems with real observations.

Models supported by DART

A full list of models can be found here, but in brief the models supported by DART include:

Model	Latest version	Model	Latest version
lorenz_63	Manhattan	lorenz_84	Manhattan
lorenz_96	Manhattan	lorenz_96_2scale	Manhattan
lorenz_04	Manhattan	simple_advection	Manhattan
bgrid_solo	Manhattan	WRF	Manhattan
MPAS	Manhattan	ATM	Manhattan
ROMS	Manhattan	CESM	Manhattan
CAM-FV	Manhattan	CAM-CHEM	Manhattan
WACCM	Manhattan	WACCM-X	Manhattan
CICE	Manhattan	CM1	Manhattan
FESOM	Manhattan	NOAH-MP	Manhattan
WRF-Hydro	Manhattan	GCCOM	Lanai
LMDZ	Lanai	MITgcm_ocean	Lanai
NAAPS	Lanai	AM2	Lanai
CAM-SE	Manhattan	CLM	Manhattan
COAMPS	Lanai	COSMO	Lanai
Dynamo	Lanai	GITM	Lanai
Ikeda	Lanai	JULES	Lanai
MPAS_ocean	Lanai	null_model	Lanai
openggcm	Lanai	PARFLOW	Lanai
sqg	Lanai	TIE-GCM	Lanai
WRF-CHEM	Lanai	ECHAM	Prior to Lanai
PBL_1d	Prior to Lanai	MITgcm_annulus	Prior to Lanai
forced_barot	Prior to Lanai	pe2lyr	Prior to Lanai
ROSE	Prior to Lanai	CABLE	Prior to Lanai

The models listed as “Prior to Lanai” will take some additional work to integrate with a supported version of DART; please contact the dart @ ucar.edu team for more information. The versions listed as “Lanai” will be ported to the Manhattan version of DART depending on the needs of the user community as well as the availablity of resources on the DART team.

Observation converters provided by DART

Given a way to compute the expected observation value from the model state, in theory any and all observations can be assimilated by DART through the obs_seq.out file. In practice this means a user-defined observation converter is required. DART provides many observation converters to make this process easier for the user. Under the directory DART/observations/obs_converters there are multiple subdirectories, each of which has at least one observation converter. The list of these directories is as follows:

Observation	Directory	Format
Atmospheric Infrared Sounder satellite retrievals	AIRS	HDF-EOS
Advanced Microwave Sounding Unit brightness temperatures	AIRS	netCDF
Aviso: satellite derived sea surface height	Aviso	netCDF
Level 4 Flux Tower data	Ameriflux	Comma-separated text
Ameriflux Fullset Flux Tower data from AmeriFlux	Ameriflux	Comma-separated text
Level 2 soil moisture from COSMOS	COSMOS	Fixed-width text
Doppler wind lidar	DWL	ASCII text
GPS retrievals of precipitable water	GPSPW	netCDF
GSI observation file	GSI2DART	Fortran binary
Global Temperature-Salinity Profile Program (GTSPP)	GTSPP	netCDF
Meteorological Assimilation Data Ingest System (MADIS)	MADIS	netCDF
MIDAS ionospheric obs	MIDAS	netCDF
MODIS satellite retrievals	MODIS	Comma-separated text
NCEP PREPBUFR	NCEP/prep_bufr	PREPBUFR
NCEP ASCII observations	NCEP/ascii_to_obs	NCEP text files
ROMS verification observations	ROMS	netCDF
Satellite winds from SSEC	SSEC	ASCII text
Sea surface temperature	SST	netCDF
Solar-Induced Fluorescence	SIF	netCDF
Special Sensor Ultraviolet Spectrographic Imager (SSUSI) retrievals	SSUSI	netCDF
World Ocean Database (WOD)	WOD	World Ocean Database packed ASCII
National Snow and Ice Data Center sea ice obs	cice	Binary sea ice
VTEC Madrigal upper atmospheric obs	gnd_gps_vtec	ASCII text
GPS obs from COSMIC	gps	netCDF
Oklahoma Mesonet MDF obs	ok_mesonet	Oklahoma Mesonet MDF files
QuikSCAT scatterometer winds	quikscat	HDF 4
Radar reflectivity/radial velocity obs	Radar	WSR-88D (NEXRAD)
MODIS Snowcover Fraction obs	snow	General text
Text file (e.g. spreadsheet) obs	Text	General text
Total precipitable water from AQUA	tpw	HDF-EOS
Automated Tropical Cyclone Forecast (ATCF) obs	Tropical Cyclones	Fixed width text
LITTLE_R obs	var	little-r
MM5 3D-VAR radar obs	var	MM5 3D-VAR 2.0 Radar data files

Data assimilation algorithms available in DART

DART allows users to test the impact of using multiple different types of algorithms for filtering, inflation/deflation, and covariance localization.

DART offers numerous filter algorithms in the Quantile-Conserving Ensemble Filter Framework. These determine how the prior distribution is updated based on the observations. The following table lists the filters supported in DART.

Filter #	Filter Name	References
1	EAKF (Ensemble Adjustment Kalman Filter)	Anderson, J. L., 2001. [1] Anderson, J. L., 2003. [2] Anderson, J., Collins, N., 2007. [3]
2	ENKF (Ensemble Kalman Filter)	Evensen, G., 2003. [4]
3	Kernel filter
4	Observation Space Particle filter
5	Random draw from posterior	None. IMPORTANT: (contact dart @ ucar.edu before using)
6	Deterministic draw from posterior with fixed kurtosis	None. IMPORTANT: (contact dart @ ucar.edu before using)
7	Boxcar kernel filter
8	Rank Histogram filter	Anderson, J. L., 2010. [5]
9	Particle filter	Poterjoy, J., 2016. [6]

DART also has several inflation algorithms available for both prior (the first value in the namelist) and posterior (the second value in the namelist). The following table lists the inflation “flavors” supported in DART along with their type number (set by inf_flavor in input.nml under the “filter_nml” section):

Flavor #	Inflation flavor name	References
0	No inflation	n/a
1	(Not Supported)	n/a
2	Spatially-varying state-space (Gaussian)	Anderson, J. L., 2009. [7]
3	Spatially-fixed state-space (Gaussian)	Anderson, J. L., 2007. [8]
4	Relaxation to prior spread (posterior inflation only)	Whitaker, J.S. and T.M. Hamill, 2012. [9]
5	Enhanced spatially-varying state-space (inverse gamma)	El Gharamti M., 2018. [10]

DART has the ability to correct for sampling errors in the regression caused by finite ensemble sizes. DART’s sampling error correction algorithm (and localization algorithm) is described in Anderson, J.L., 2012 [11] Sampling error correction can be turned on or off via the sampling_error_correction variable in the input.nml under the “assim_tools_nml” section.

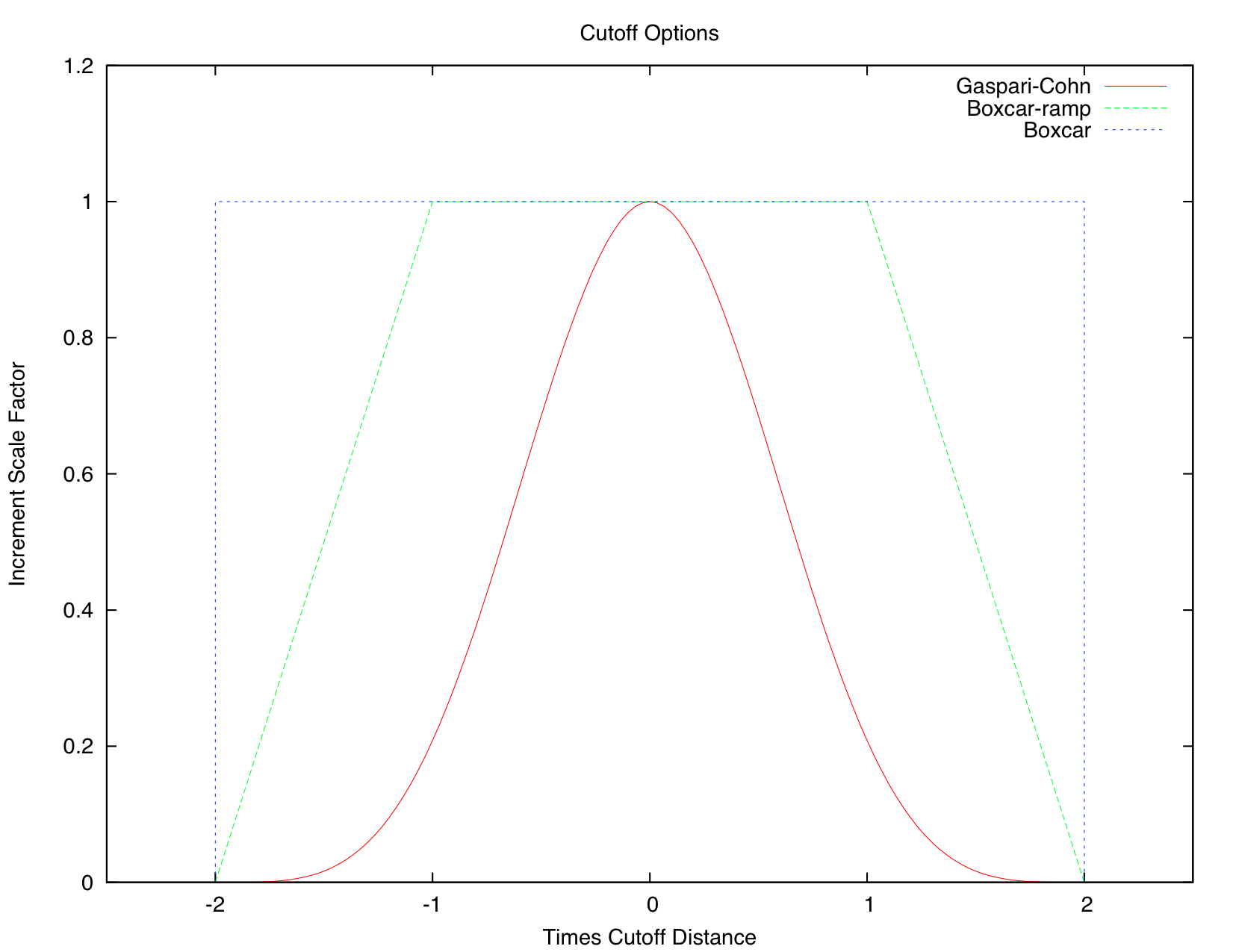
The following covariance localization options are available (set by select_localization in input.nml under the “cov_cutoff_nml” section):

Loc #	Localization type	References
1	Gaspari-Cohn eq. 4.10	Gaspari, G. and Cohn, S. E., 1999. [12]
2	Boxcar	None
3	Ramped boxcar	None

The following image depicts all three of these options:

References

[1]

Anderson, J. L., 2001: An Ensemble Adjustment Kalman Filter for Data Assimilation. Monthly Weather Review, 129, 2884-2903. doi:10.1175/1520-0493(2001)129<2884:AEAKFF>2.0.CO;2

[2]

Anderson, J. L., 2003: A local least squares framework for ensemble filtering. Monthly Weather Review, 131, 634-642. doi:10.1175/1520-0493(2003)131<0634:ALLSFF>2.0.CO;2

[3]

Anderson, J., Collins, N., 2007: Scalable Implementations of Ensemble Filter Algorithms for Data Assimilation. Journal of Atmospheric and Oceanic Technology, 24, 1452-1463. doi:10.1175/JTECH2049.1

[4]

Evensen, G., 2003: The Ensemble Kalman Filter: Theoretical Formulation and Practical Implementation. Ocean Dynamics. 53(4), 343–367. doi:10.1007%2Fs10236-003-0036-9

[5]

Anderson, J. L., 2010: A Non-Gaussian Ensemble Filter Update for Data Assimilation. Monthly Weather Review, 139, 4186-4198. doi:10.1175/2010MWR3253.1

[6]

Poterjoy, J., 2016: A localized particle filter for high-dimensional nonlinear systems. Monthly Weather Review, 144 59-76. doi:10.1175/MWR-D-15-0163.1

[7]

Anderson, J. L., 2009: Spatially and temporally varying adaptive covariance inflation for ensemble filters. Tellus A, 61, 72-83, doi:10.1111/j.1600-0870.2008.00361.x

[8]

Anderson, J. L., 2007: An adaptive covariance inflation error correction algorithm for ensemble filters. Tellus A, 59, 210-224, doi:10.1111/j.1600-0870.2006.00216.x

[9]

Whitaker, J.S. and T.M. Hamill, 2012: Evaluating Methods to Account for System Errors in Ensemble Data Assimilation. Monthly Weather Review, 140, 3078–3089, doi:10.1175/MWR-D-11-00276.1

[10]

El Gharamti M., 2018: Enhanced Adaptive Inflation Algorithm for Ensemble Filters. Monthly Weather Review, 2, 623-640, doi:10.1175/MWR-D-17-0187.1

[11]

Anderson, J.L., 2012: Localization and Sampling Error Correction in Ensemble Kalman Filter Data Assimilation. Monthly Weather Review, 140, 2359–2371. doi:10.1175/MWR-D-11-00013.1

[12]

Gaspari, G. and Cohn, S. E., 1999: Construction of correlation functions in two and three dimensions. Quarterly Journal of the Royal Meteorological Society, 125, 723-757. doi:10.1002/qj.49712555417