Verifying installation
Note
These verification steps require MATLAB®. UCAR Member Institutions have access to institutional licenses for MATLAB, thus we have created verification tools using it.
The Lorenz model is notoriously sensitive to very small changes; in fact, the story of Lorenz discovering this sensitivity is a classic in the annals of the study of chaos, which in turn was instrumental in the development of data assimilation as a field of study. See The Lorenz 63 model: what is it and why should we care? or What is data assimilation? for more information.
This sensitivity is of practical interest for verifying these results. The initial conditions files and observations sequences are provided in ASCII, which is portable across systems, but there may be some machine-specific round-off error in the conversion from ASCII to machine binary. As Lorenz 63 is such a nonlinear model, extremely small differences in the initial conditions may eventually result in noticeably different model trajectories. Even different compiler flags may cause tiny differences that ultimately result in large differences. Your results should start out looking VERY SIMILAR and may diverge with time.
The simplest way to determine if the installation is successful is to
run some of the functions available in DART/diagnostics/matlab/.
Usually, we launch MATLAB from the DART/models/lorenz_63/work
directory and use the MATLAB addpath command to make the
DART/matlab/ functions available for execution in any working
directory.
In the case of this Lorenz model, we know the “true” (by definition) state of the model that is consistent with the observations, which was generated by the perfect_model_obs program as described in Checking the build — running something. The following MATLAB scripts compare the ensemble members with the truth and can calculate the error in the assimilation:
$ cd DART/models/lorenz_63/work
$ matlab -nodesktop
(Skipping startup messages)
[matlab_prompt] addpath ../../../diagnostics/matlab
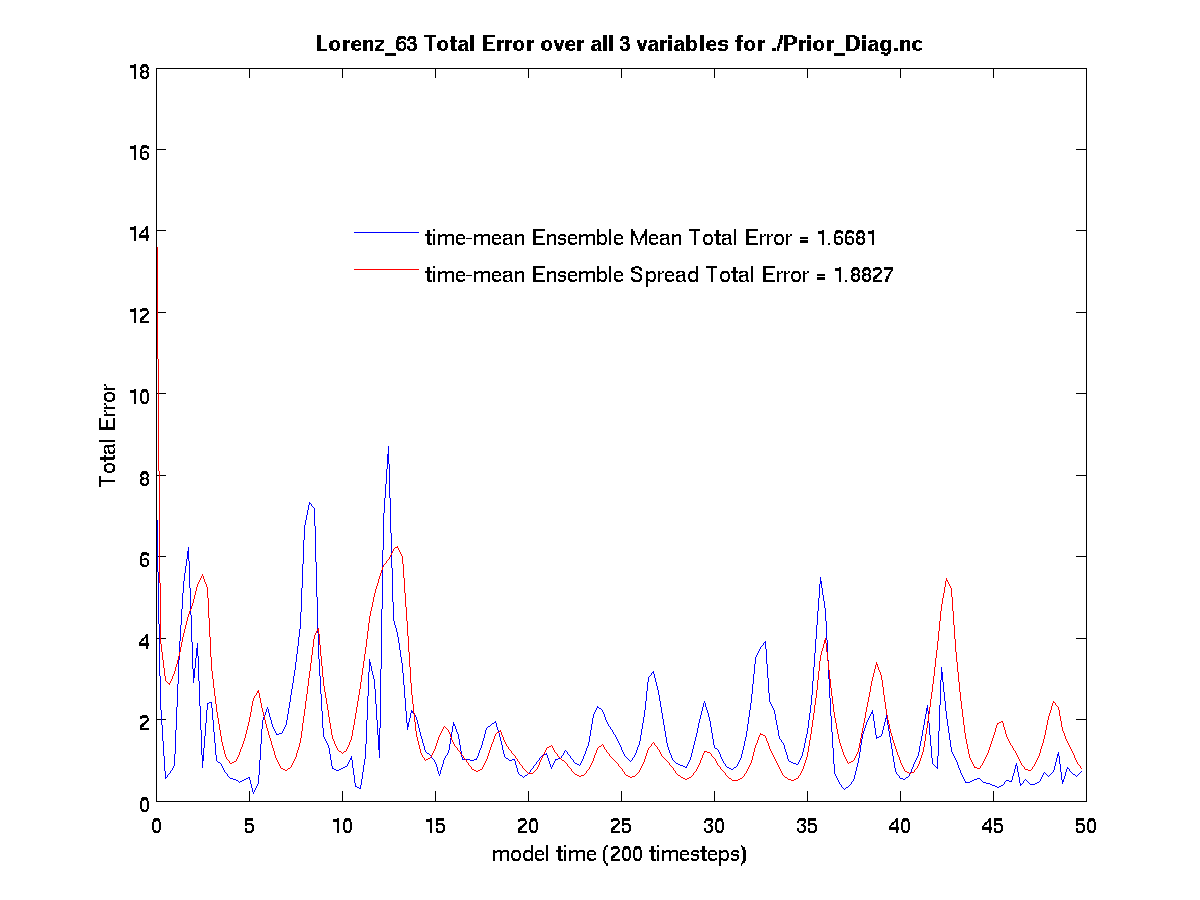
[matlab_prompt] plot_total_err
Input name of true model trajectory file;
(cr) for perfect_output.nc
perfect_output.nc
Input name of ensemble trajectory file;
(cr) for preassim.nc
preassim.nc
Comparing true_state.nc and
preassim.nc
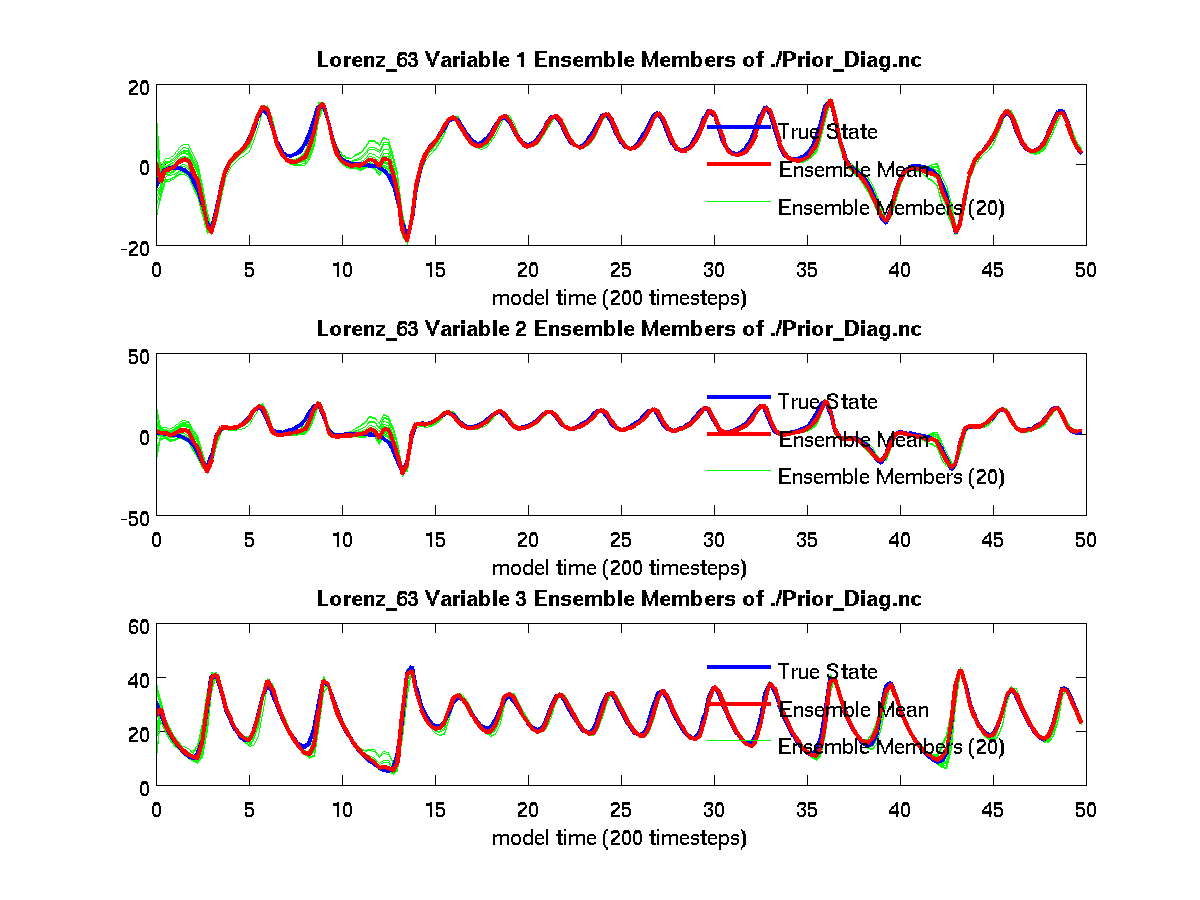
[matlab_prompt] plot_ens_time_series
Input name of ensemble trajectory file;
(cr) for preassim.nc
Comparing true_state.nc and
preassim.nc
Using Variable state IDs 1 2 3
pinfo =
struct with fields:
model: 'Lorenz_63'
def_var: 'state'
num_state_vars: 1
num_copies: 20
num_ens_members: 20
ensemble_indices: [1 2 3 ... 18 19 20]
min_state_var: 1
max_state_var: 3
def_state_vars: [1 2 3]
fname: 'preassim.nc'
truth_file: 'true_state.nc'
diagn_file: 'preassim.nc'
truth_time: [1 200]
diagn_time: [1 200]
vars: {'state'}
time: [200x1 double]
time_series_length: 200
var: 'state'
var_inds: [1 2 3]
From the above plot_ens_time_series graphic, you can see the
individual green ensemble members becoming more constrained with less
spread as time evolves. If your figures look similar to these, you
should feel confident that everything is working as intended. Don’t miss
the opportunity to rotate the “butterfly” plot for that classic chaos
theory experience (perhaps while saying, “life, uh, finds a way”).
Congratulations! You have now successfully configured DART and are ready to begin the next phase of your interaction with DART. You may wish to learn more about:
What is data assimilation? — a brief introduction to ensemble data assimilation. This section includes more information about the Lorenz 63 model and how to configure the
input.nmlfile to play with DA experiments in DART using the Lorenz 63 model.What is DART? — This section includes more information about DART and a basic flow chart of the overall DART workflow.
Note
In the case that the above instructions had one or more issues that either did not work for you as intended or were confusing, please contact the DART software development team at dart@ucar.edu. We value your input to make getting started as smooth as possible for new DART users!